The functional zipper structure

There is a problem called tree manager in HackerRank functional domain . In shorts, there is a tree structure, which has sibling and parent, and there are different operations like visitParent, visitChild, go to left sibling etc which change the current focus of the root node in the tree.

It is clear that this problem can be solved using a imperative data structure, we can use point to point to the parent of current node, and store the children as a array or linked-list for current node. For most operation in the the problem ,it will require $O(1)$ time complexity, only for operation like visitChild(n) ,insertLeft(x), insertRight(x), visitChild(n) which may be proportional to the length of the children depends on the data structure you use to store the children. But since the maximum length of children of a node is 10, it would be enough to solve this problem in the time requirements.

The problem is how can we solve this in an idiom functional way. One easy way is just to use some mutable structure like in imperative language. Another way is to store the structure as a tree, and every update operation we change the whole path from the current focus to the root what we normally do in a persistent data structure. But this approach has a problem, if the tree degenerate into a linked list, every update operation will require $O(n)$ , where $n$ is the length from the root to the current focus, which will cause the worst case of this problem to become $O(Q^2)$ , which will definitively not be able to pass in the worst case.

As the following image shows, if we change the node of $6$ to $6'$ in the tree, although we do not change the value of $1$ and $3$ in the tree, but to make the tree persistent, we need to create all the ancestors node from $6$ to the root to create a new path. In the image, all the circle node and the red paths need to be maintained during the update operation.

Persistent tree structure .

The solution is a very elegant functional structure I learned during solving this problem which is I want to share in the post.

The structure is called zipper, which can be use in one dimensional list or in a tree structure. For how to use the zipper in a tree structure, there is a paper which describe how to use the structure in a tree. In this post, I will try to give a more detailed and intuitive explanation of the structure.

Suppose we have a structure, in this structure we have a current focus(you can imagine this focus as a pointer point to some node in this structure).

For example, in one dimension, you can imagine the structure as an array or list , and there is a pointer point to some position in the list, and we can change the current focus to the left, right, add/insert items to the left, right etc.

In a tree form, we can think this as a directory tree in file system, we can go parent directory, go to nth child of current directory, and the current focus is just the current directory at any time.

Let us think first how to solve this problem in one dimension in a functional way. The naive idea is to use a linked list to store the item, and hold the current focus. This will make all operations to the right like switch focus to the right and add item to the current right in $O(1)$ time. But to add item to the left, or switch focus to the left would require copy the node from the beginning to the current node or traverse from the beginning to the current node as show in the following picture, which will make these operations proportional to the depth of current node in the list. In the picture, the current focus is at node 6, if we want to insert a 5 as its left sibling, we need to copy the whole path from the beginning to the current node.

List insert left

How can we use a efficient functional structure to do all these operations? The solution is amazingly simple, we store the structure in a tuple, the first element is a list of the left sibling of current focus in reverse order, the second item is the current focus, while the third item is the right sibling. For example, the above example will be something like ([4; 3; 2; 1], 6, [7; 8]). And this is also how the name zipper came from, because the structure looks like a zipper. For example, if we continue apply goLeft operation to the structure, it will become ([3; 2; 1],4,[6; 7; 8]), ([2; 1],3, [4;6;7;8]), ([1],2,[3; 4; 6; 7; 8]) and finally become ([],1,[2; 3; 4; 6; 7; 8]), something like an zipper go from open to closed status.

All the operations are show as the following code snipe.

(* left_reverse * current * right *)
type 'a zipper = Zipper of ('a list) * 'a * ('a list)

let goLeft = function
    | Zipper([], _, _) -> failwith "left of leftmost element"
    | Zipper(l :: ls, y, rs) -> Zipper(ls, l, y :: rs)

let goRight = function
    | Zipper(_, _, []) -> failwith "right of rightmost element"
    | Zipper(ls, x, y :: rs) -> Zipper(x :: ls, y, rs)

let insertLeft y = function
    | Zipper(ls, x, rs) -> Zipper(y :: ls, x, rs)

let insertRight y = function
    | Zipper(ls, x, rs) -> Zipper(ls, x, y :: rs)

We defined the zipper as a some kind of a 3 elements tuple, as said above, the first element store the left siblings of current focus in reverse order, the second element is the focus itself, and the right element is the right siblings. Since we know that in functional language, it is very cheap to do operation at the header of list, so all the above operations are $O(1)$ in complexity.

To use this structure in a tree described in the problem is very simple, The only additional information we need to maintain are the parent relation in tree and the sons of the current node, as defined in the following type definition.

(* [left(reversed)] * parent * [right] * value * [children] *)
type 'a path =
    | Top
    | PathNode of ('a path list) * ('a path)  * ('a path list) * 'a * ('a path list)

As the above definition, a path is either a Top or a five elements tuple which hold the reverse left siblings, the parent, the right siblings, the current value and the sons of current node.

And all the operations are quite similar to the linear zipper. The only operations which is not $O(1)$ is goUp, nth and delete as show bellow, since they either need to go through a list to find the nth element or re-construct the information of children nodes of the parents because we use a zipper structure to store them.

let goUp p =
    match p with
    | Top -> failwith "up of top element"
    | PathNode(left, up, right, _, _) ->
        match up with
        | Top -> failwith "up with top"
        | PathNode(left', up', right', value, _) ->
            PathNode(left', up', right', value, (List.rev left) @ (p :: right))

let rec nth p = function
    | 1 -> goDown p
    | n when n > 0 -> goRight (nth p (n - 1))
    | _ -> failwith "n must be greater or equal to zero"

let delete p =
    match p with
    | Top -> failwith "delete of path top"
    | PathNode(left, up, right, _, _) ->
        match up with
        | Top -> failwith "delete the root node"
        | PathNode(left', up', right', curValue, _) ->
            PathNode(left', up', right', curValue, (List.rev left) @ right)

But since depend on the structure we use in a imperative way, we also has several operations which require $O(length)$ time complexity, where length is the number of children node of one element. We already achieve the same time complexity as we can do in a imperative way.

Actually, the zipper structure is very similar to the functional queue, which also split the structure into two part, and also need to reverse part of the structure. The dequeue operation’s worst case is $O(n)$ , but it can guarantee that each operation take only $O(1)$ amortized time.

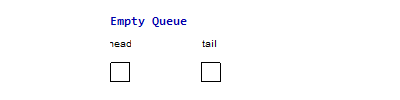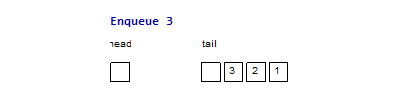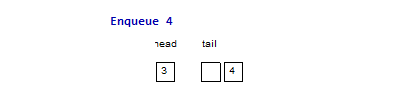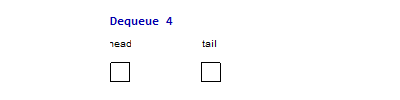
For example, the following two images are the imperative & functional queues doing the same operation sequence enqueue(1), enqueue(2), enqueue(3), dequeue(), dequeue(), enqueue(4), dequeue(), dequeue(). The functional queue use two list to maintain the head & tail part of the queue, normally the operation only happen at the head of one list, only when the head list is empty and we do a dequeue() operation, we need to reverse the tail part to become the head part, but since every element will at most reverse once from the tail part to the head part, it is easy to prove that the amortized complexity is $O(1)$ . And for the imperative queue, since it can have random access of element in $O(1)$ time, so all the operations are just in constant time complexity.

Imperative Queue	Functional Queue

Final thought

Although I admit that functional programming is more easy to reason the correctness and generally the program is more concise and elegant, but I still think that every paradigm has its own strength and weakness. For this specific example, I think it would be much easier to implement this problem in an imperative way instead of design the structure from scratch(if someone has never be shown any of the functional queue structure or zipper structure, I would doubt the probability of coming out this idea by himself). That’s why I really appreciated language like F# since it allow you to use multiple paradigms in one language, and will have strengths from different program paradigms.

You can view the whole program at hackerrank/Tree-Manager.

m00nlight 17 December 2017

Next Post → ← Earlier Post

Lisp Is Smart Programming ← m00nlight

The functional zipper structure

Final thought