Nonogram prolog clpb solution
Recently, I was introduced the nonogram problem by some of my friends. And it seems to be another example where constraint programming really shines. So in this post, I will show you how you could solve the problem using SWI prolog’s clpb library in about 50 lines of code.
Problem
The problem statement is really simple, you have a board to fill in black or white, and the problem give the constraints of each row and each columns, based on the constraints, you need to figure out how to fill the board.
The constraints is just the numbers of continuous black in each row and columns.
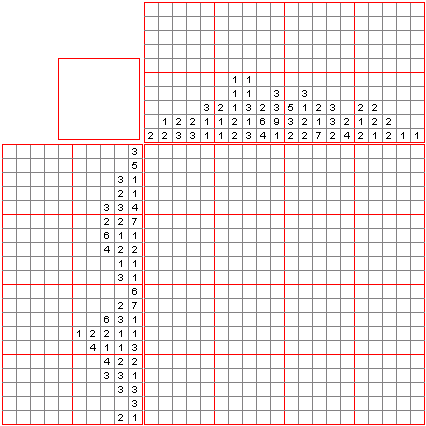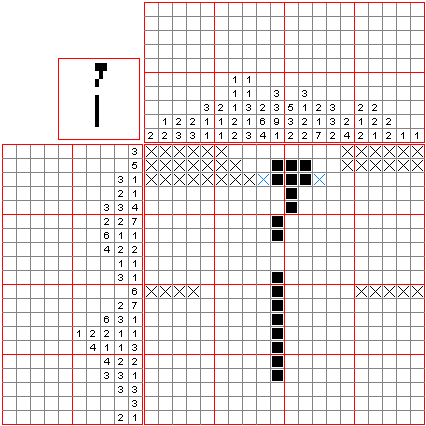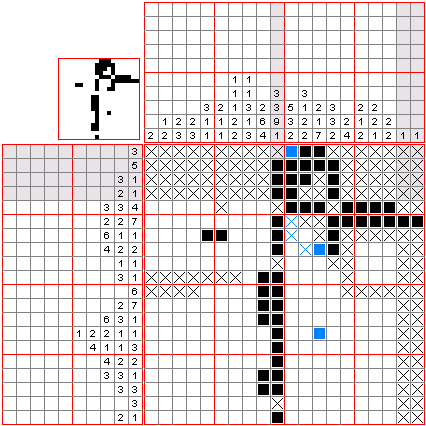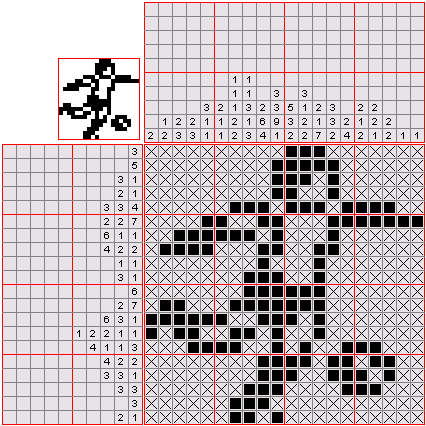
Example from wiki
Solution
Based on the problem statement, we first need to build the constraints of the problem. At first, it is not very clear how can we build the constraints of the problem. But after some search on the internet, I came across a solution in another constraint programming framework Gecode, which build the constraints using regular expression.
For example, if we use 0 as false and 1 as true, and the constraint is
[3, 2, 2], the row as a string should be in regular expression form like
0*1{3}0+1{2}0+1{2}0*.
So I want to follow the same approach to solve it in Prolog. Prolog’s definite clause grammar(DCG) make it really easy to build a small regular expression engine. The following code is of some minor modification of this stackoverflow answer. For users who are not familiar with Prolog’s DCG, please refer to some tutorial here.
:- op(100, xf, *).
:- op(100, xf, +).
:- op(100, xfy, **).
regex(C) --> [C].
regex([T|Ts]) --> regex(T), regex(Ts).
regex([]) --> [].
regex(eps) --> [].
regex(_*) --> [].
regex(R*) --> regex(R), regex(R*).
regex(R+) --> regex(R), regex(R*).
regex((R1|R2)) --> ( regex(R1) ; regex(R2) ).
regex(range(R,N,M)) -->
{between(N,M,L),
length(D,L),
maplist(copy_term(R),D)
}, regex(D).
regex(repeat(R, N)) -->
length(D, N),
maplist(copy_term(R), D),
regex(D).
regex(R**N) --> regex(range(R, N, N)).
Use the above code, we can match a list with a regular expression like
?- phrase(regex([0*,1**3, 0+, 1**2, 0+]), [1, 1, 1, 0, 1, 1]).
false.
?- phrase(regex([0*,1**3, 0+, 1**2, 0+]), [1, 1, 1, 0, 1, 1, 0]).
true ;
false.
Or generate all sequences which satisfy the regular expression like
?- use_module(library(clpb)).
true.
?- length(Row, 8), phrase(regex([0*, 1**3, 0+, 1**2, 0+]), Row), labeling(Row).
Row = [1, 1, 1, 0, 1, 1, 0, 0] ;
Row = [1, 1, 1, 0, 0, 1, 1, 0] ;
Row = [0, 1, 1, 1, 0, 1, 1, 0] ;
false.
Now we can build the constraints construction of the problem. The following code will change one row or column’s constraint to the regular expression form.
constraint_2_regex_tail([], [0*]) :- !.
constraint_2_regex_tail([H|T], [0+, 1**H | TRes]) :-
constraint_2_regex_tail(T, TRes).
constraint_2_regex([], [0*]) :- !.
constraint_2_regex([X], [0*, 1**X, 0*]) :- !.
constraint_2_regex([H|T], [0*, 1**H| RegexTail]) :-
constraint_2_regex_tail(T, RegexTail).
Using the previous [3,2,2] as an example, the constraint_2_regex will
generate something like
?- constraint_2_regex([3, 2, 2], Res).
Res = [0*, 1**3, + 0, 1**2, + 0, 1**2, 0*].
I don’t know why there is some problem of display 0+ as + 0, but it
is actually the correct regular expression.
?- constraint_2_regex([3, 2, 2], Regex), length(Row, 9), phrase(regex(Regex), Row),
| labeling(Row), writeln(Row).
[1,1,1,0,1,1,0,1,1]
Regex = [0*, 1**3, + 0, 1**2, + 0, 1**2, 0*],
Row = [1, 1, 1, 0, 1, 1, 0, 1, 1] ;
false.
?- constraint_2_regex([3, 2, 2], Regex), length(Row, 10), phrase(regex(Regex), Row),
| labeling(Row), writeln(Row).
[1,1,1,0,1,1,0,1,1,0]
Regex = [0*, 1**3, + 0, 1**2, + 0, 1**2, 0*],
Row = [1, 1, 1, 0, 1, 1, 0, 1, 1|...] ;
[1,1,1,0,1,1,0,0,1,1]
Regex = [0*, 1**3, + 0, 1**2, + 0, 1**2, 0*],
Row = [1, 1, 1, 0, 1, 1, 0, 0, 1|...] ;
[1,1,1,0,0,1,1,0,1,1]
Regex = [0*, 1**3, + 0, 1**2, + 0, 1**2, 0*],
Row = [1, 1, 1, 0, 0, 1, 1, 0, 1|...] ;
[0,1,1,1,0,1,1,0,1,1]
Regex = [0*, 1**3, + 0, 1**2, + 0, 1**2, 0*],
Row = [0, 1, 1, 1, 0, 1, 1, 0, 1|...] ;
false.
Finally, here are the part to solve the nonogram.
sat_row(Row, Cs) :-
constraint_2_regex(Cs, RegCs),
phrase(regex(RegCs), Row),
labeling(Row).
same_col_length([], _).
same_col_length([H|T], N) :-
length(H, N),
same_col_length(T, N).
nonogram(Rows, RowCs, ColCs) :-
length(RowCs, RowLen), length(Rows, RowLen),
length(ColCs, ColLen), same_col_length(Rows, ColLen),
maplist(constraint_2_regex, RowCs, RowCsRegex),
maplist(constraint_2_regex, ColCs, ColCsRegex),
transpose(Rows, Cols),
maplist(sat_row, Rows, RowCsRegex),
maplist(sat_row, Cols, ColCsRegex).
And here are some simple test cases.
test(1, _,
[[], [3], [1, 1], [3], [1]],
[[], [], [4], [1, 1], [3]]).
test(2, _,
[[4], [1, 1], [4], [1], [5], [1]],
[[], [5], [1, 1, 1], [1, 1, 2], [3, 1], [1]]).
test(3, _,
[[], [4], [6], [2, 2], [2, 2], [6], [4], [2], [2], [2], []],
[[], [9], [9], [2, 2], [2, 2], [4], [4], []]).
You can test it like
?- test(N, Rows, RowCs, ColCs), nonogram(Rows, RowCs, ColCs), maplist(writeln, Rows).
[0,0,0,0,0]
[0,0,1,1,1]
[0,0,1,0,1]
[0,0,1,1,1]
[0,0,1,0,0]
N = 1,
Rows = [[0, 0, 0, 0, 0], [0, 0, 1, 1, 1], [0, 0, 1, 0, 1], [0, 0, 1, 1, 1], [0, 0, 1, 0|...]],
RowCs = [[], [3], [1, 1], [3], [1]],
ColCs = [[], [], [4], [1, 1], [3]] ;
[0,1,1,1,1,0]
[0,1,0,0,1,0]
[0,1,1,1,1,0]
[0,1,0,0,0,0]
[0,1,1,1,1,1]
[0,0,0,1,0,0]
N = 2,
Rows = [[0, 1, 1, 1, 1, 0], [0, 1, 0, 0, 1, 0], [0, 1, 1, 1, 1, 0], [0, 1, 0, 0, 0|...]\
[0, 1, 1, 1|...], [0, 0, 0|...]],
RowCs = [[4], [1, 1], [4], [1], [5], [1]],
ColCs = [[], [5], [1, 1, 1], [1, 1, 2], [3, 1], [1]] ;
Some though on efficiency
Although it is really elegant to solve this problem in SWI-Prolog’s clpb library, the problem is not extremely efficient. For example, the third test will take around 10 minutes to find several answers on my desktop with an I7 processor. But since this problem is an NP problem, it is not that bad(the third problem should be of time complexity of 2^88). But we should know that in practice,
Many nonogram problems can be solved efficiently, because the interrelated constraints on the two axes allow the search space to be bounded, dramatically reducing the space that must be searched for a solution. Nonogram Wiki
And if anyone knows more efficient way to solve this in Prolog’s clpb. you are welcome to tell me :).
Here I don’t intent to make the program the most efficient to solve the problem, I just want to show how elegant the problem can be solved in the constraint programming paradigm.
You can find the whole program on clpb-nonogram.
m00nlight 22 September 2016